CAPITULO 3

Ejercicios.

3.3. Concatenación.

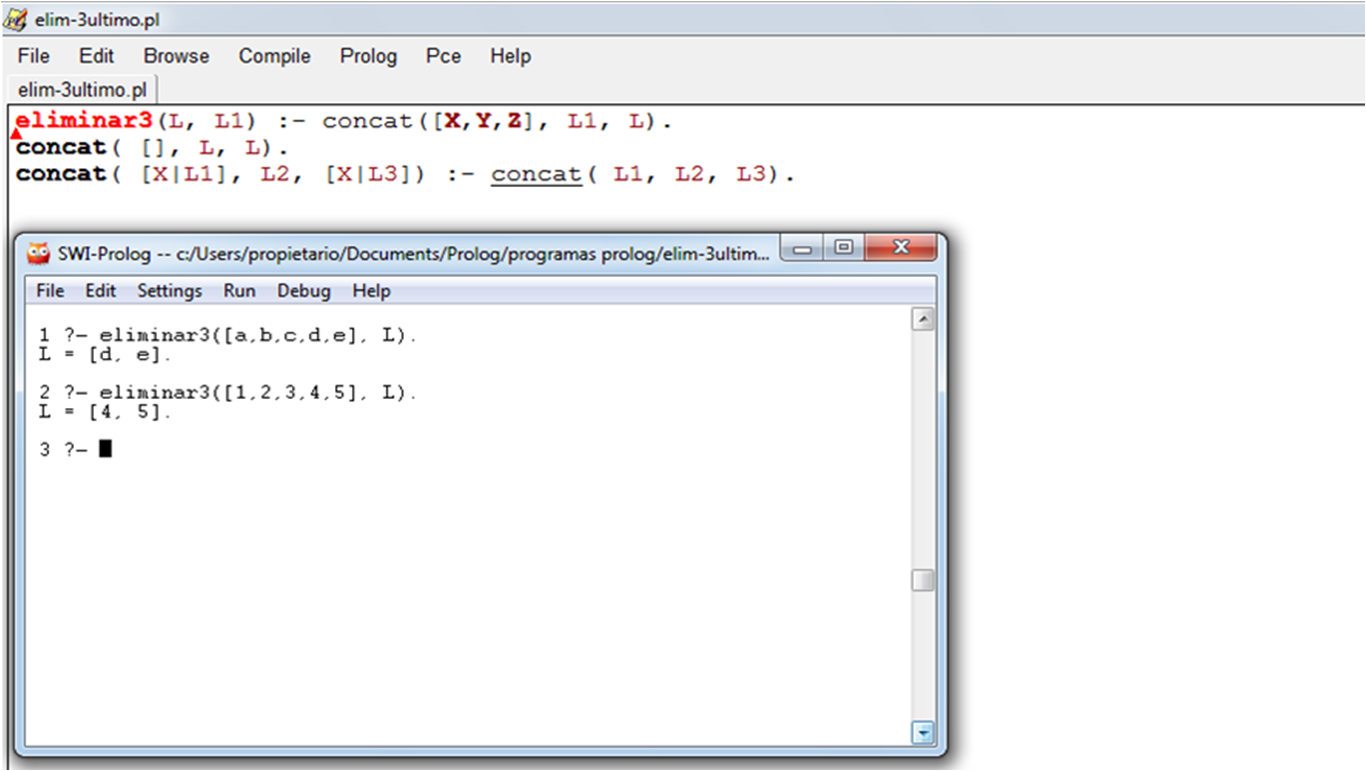
1. Escriba una meta, usando concat, para eliminar los tres últimos elementos de una lista
L produciendo otra lista L1. Recomendación: L es la concatenación de L1 y una lista de
tres elementos.

2. Escriba una secuencia de metas para eliminar los tres primeros elementos y los tres
últimos elementos de una lista L produciendo la lista L2.

3. Defina la relación:
ultimo( Elemento, Lista)
de tal modo que Elemento sea el último elemento de la lista Lista. Escriba dos versiones:
(a) usando la relación concat, y (b) sin usarla.


PREGUNTEMOS:

1 ?-  ultimo(d,[a,c,e,f,d,f]).

false.

2 ?- ultimo(a,[d,e,g,h,f,a]).

true .

3 ?- ultimo(a,[a,a,a,a,a,a,a,a]).

true .

4 ?- ultimo(6,[2,3,4,5,1,7,6,2]).

false.

5 ?- ultimo(pedro,[alejandro,carlos,alberto,antonio,pedro]).

true .

PREGUNTEMOS:

1 ?-  eliminaultimo( [x,y,z,r,s,t], X, L).

2 ?-  eliminaultimo( [1,2,3,4,5,6], 7, L).

3.4. Aritmética.

1. Defina la relación max(X,Y,Max) de tal modo que Max sea< el mayor valor de los
dos números X y Y.
max(X,Y,Max).
max(X,Y,Max):-X<Max,Y<Max.

2. Defina el predicado maxlist(List, Max) de tal manera que Max sea el mayor
número de la lista List de números.
maxlist(List,Max).
maxlist(List,Max):-Max>List.
3. Defina el predicado sumlist(List, Sum) donde Sum es la suma de una lista de
números dada en List.
sumlist(List,Sum).
List([X,Y,Z]).
sumlist(List,Sum):-X is Y is Z=:=Sum.
4. Defina el predicado ordenada(List) el cual es cierto (devolverá yes) si List es una
lista ordenada de números en forma ascendente o descendente, por ejemplo,
?- ordenada(1,5,6,6,9,12).
Yes
ordenada(List).
List(X,Y,Z).
ordenada(List):-X<Y<Z=:=ascendente.
ordenada(List):-X>Y>Z=:=descendente.
5. Defina el predicado subsum(Set, Sum, Subset) donde Set es una lista de números,
Subset es un subconjunto de esta lista y Sum es la suma de los números en
Subset. Por ejemplo,
?- subsum([1,2,5,3,2], 5, Sub).
Sub = [1,2,2];
Sub = [2,3];

Sub = [5];
subsum(set,Sum,Subset).
subsum(Set,Sum,Subset):-Set=:=[X,Y,Z],Sum=:= Y,Subset=:=Sub.

EJERCICIOS (Capitulo 2)

2.4. Significado procedural.
1. Considere el programa anterior y realize la traza de ejecución a la pregunta :
?- enorme(X), oscuro(X).
compare su traza de ejecución con la anterior, ya que esencialmente es la misma pregunta pero con otro orden. ¿En cuál de ambos casos Prolog realiza más trabajo antes de encontrar la respuesta final?

Recordemos:
(a). Programa.
enorme( oso). % cláusula 1
enorme( elefante). % cláusula 2
chico( gato). % cláusula 3
cafe( oso). % cláusula 4
negro( gato). % cláusula 5
gris( elefante). % cláusula 6
oscuro( Z) :- % cláusula 7 : cualquier negro es oscuro.
negro( Z).
oscuro( Z) :- % cláusula 8 : cualquier café es oscuro.
cafe( Z).
(b). Pregunta.

?- enorme( X), oscuro( X). % Quién es oscuro y enorme ?

 (c).Traza de la Ejecución

 1)    Lista inicial de metas: enorme(X), oscuro(X).

 2)    Examina el programa de arriba hacia abajo buscando una cláusula

cuya cabeza empate con la primera meta:

enorme (X)

Se encuentra la cláusula 1: enorme (oso).

Esta cláusula no tiene cuerpo, así que la lista de metas, luego de

instanciarse se convierte en:            

 oscuro(oso)

 3)    Examina el programa para buscar la meta oscuro(oso), encuentra la 

cláusula 7 que luego de instanciarse se convierte 

 enorme(oso),negro(oso)

4)    Examina el programa para buscar la meta negro(oso), no se

encuentra ninguna cláusula. 

Por lo tanto se realiza un proceso de backtracking al paso 3) y 

se elimina la instanciación 

negro(oso)

 Se continúa examinando el programa a partir de la cláusula 7.

5)Examina el programa para buscar la meta oscuro(oso), encuentra la cláusula 8 que

luego de instanciarse se convierte en:

enorme(oso),cafe(oso)

Esta cláusula no tiene cuerpo, así que la lista de metas se queda vacía. 

Esto indica una terminación exitosa y la instanciación correspondiente 

a la variable queda como:

                  X = oso.

En la  traza de ejecución: oscuro(X),enorme(X)  Prolog realiza más trabajo 

antes de encontrar la respuesta final.

EJERCICIOS (Capitulo 2)

2.1. Tipos básicos de datos.

1.Sugiera una representación para rectángulos,

 cuadrados y círculos como objetos Prolog estructurados. 

Escriba algunos ejemplos que representen objetos 

físicos concretos utilizando la representación que sugirió.

Circulo(punto(X,Y),radio(X,Y))        

Rectangulo(punto(X,Y),puntoc,punto(X,Y),punto(X,Y)).

Cuadrado(punto(X,Y),punto(X,Y),punto(X,Y),punto(X,Y)).

Ejemplos:

Triangulo(punto(X,Y),punto(X,Y),punto(X,Y)).

Línea(punto(X,Y),punto(X,Y)).

Rombo(punto(X,Y),punto(X,Y),punto(X,Y),punto(X,Y)).

2.2. Matching (empatamiento).

1.¿Las siguientes operaciones de matching tienen 

éxito o fallan?,Si tienen éxito, ¿cuáles son las instanciaciones 

resultantes en las variables?

(a). punto( A, B) = punto( 1, 2).

            Tiene éxito

            Sus instanciaciones resultantes son:

A=1

            B=2

(b). punto( A, B) = punto( X, Y, Z).

            No tiene éxito

            false.

(c). +( 2, 2) = 4.

            No tiene éxito

             false.

(d). +( 2, D) = +( E, 2).

            Tiene éxito

            Sus instanciaciones resultantes son:

D=E

            E=2

(c). triangulo(punto(-1,0),P2,P3) = triangulo(P1,punto(1,0),punto(0,Y)).

            Tiene éxito

            Sus instanciaciones resultantes son:

P2 = punto(1, 0)

P3 = punto(0, Y)

P1 = punto(-1, 0)

2.3. Significado declarativo.

1 . Considere el siguiente programa:

f( 1, uno).

f( s(1), dos).

f( s(s(1)), tres).

f( s(s(s(X))), N) :- f( X, N).

¿Cómo contestará Prolog las siguientes preguntas? 

Cuando sean posibles varias respuestas, dé al menos dos de ellas.

(a). ?- f( s(1), A).

            Respuesta de Prolog:

            A=dos

(b). ?- f( s(s(1)), dos).

            Respuesta de Prolog :

           false.

(c). ?- f( s(s(s(s(s(s(1)))))), C).

            Respuesta de Prolog:

            C = uno.

(d). ?- f( D, tres).

          Respuesta de Prolog:

            D = s(s(1)).

2. El siguiente programa dice que dos personas son 

parientes si,

(a). uno es predecesor del otro, ó

(b). ambos tienen un predecesor común, ó

(c). ambos tienen un sucesor común :

parientes( X, Y) :- predecesor( X, Y).

parientes( X, Y) :- predecesor( Y, X).

parientes( X, Y) :- predecesor( Z, X), predecesor( Z, Y).

parientes( X, Y) :- predecesor( X, Z), predecesor( Y, Z).

¿ puede usted acortar el programa usando la notación de ';' ?

parientes(X,Y) :- predecesor(X,Y) ; predecesor(Y,X) ;predecesor(Z,X),

 predecesor(Z,Y) ; predecesor(X,Z) , predecesor(Y,Z).

3.Reescriba el siguiente programa sin utilizar la notación de ';' :

traducir( Numero, Palabra) :-

Numero = 1, Palabra = uno;

Numero = 2, Palabra = dos;

Numero = 3, Palabra = tres.

traducir(Numero,Palabra) :- Numero=1,Palabra=uno.

traducir(Numero,Palabra) :- Numero=2,Palabra=dos.

traducir(Numero,Palabra) :- Numero=3,Palabra =tres.

REGLAS RECURSIVAS 1.6 (Capitulo 1)

1.6.Considere las siguiente definicion alternativa de predecesor:

1).predecesor(X,Z):-progenitor(X,Z).

2).predecesor(X,Z):-progenitor(Y,Z),predecesor(X,Y).

¿Es apropiada esta definicion?

Si

¿Puede usted  dibujar una diagrama que corresponda con estas definiciones?

Diagrama de 1

Diagrama de 2

EJERCICIOS DE 1.3 REGLAS (Capitulo 1)

1.3. Traduzca las siguientes sentencias a reglas Prolog.

a). Cualquiera que tiene un hijo es feliz (introduzca la relación unaria llamada 'feliz').

X es feliz, si X es progenitor

  feliz (X) :- progenitor (X,Y)

Esta pregunta de dos pasos se puede escribir en Prolog:

?- feliz(X).

b). Para todo X, si X tiene un hijo que tiene una hermana, entonces X tiene dos hijos

(introduzca la relación tiene-dos-hijos).

tiene_dos_hijos(X,Y):-hermana(Y,Z),progenitor(X,Y),progenitor(X,Z),mujer(Z).

1.4. Defina la relación 'nieto' usando la relación 'progenitor'.

Recomendación: Será similar a la relación abuelo.

 Ahora queremos preguntar ¿quién es el nieto de roberto?

El programa no incluye la relación 'nieto', sin embargo podemos hacer la pregunta en dos pasos:

1). De Quién es progenitor roberto, asumimos que de algún Y.

2). De Quién es progenitor este Y, asumimos que de algún X.

Esta pregunta de dos pasos se puede escribir en Prolog:

?- progenitor( roberto, Y) , progenitor( Y, X ).

X = jaime

Y = patricia

En general, ¿quién es el nieto de Z?

El programa no incluye la relación 'nieto', sin embargo podemos hacer la pregunta en dos pasos:

1). De Quién es progenitor Z, asumimos que de algún Y.

2). De Quién es progenitor este Y, asumimos que de algún X.

Esta pregunta de dos pasos se puede escribir en Prolog:

?- progenitor( Z, Y) , progenitor( Y, X ).

1.5. Defina la relación tia ( X, Y) en términos de las relaciones 'progenitor' y

'hermana'. Dibuje primero un diagrama para ésta relación.

tia(X,Z):-hermana(X,Y),progenitor(Y,Z),mujer(X),diferente(X,Y).

MI ÁRBOL FAMILIAR

El siguiente árbol es mi árbol genealógico.

 Notemos que en Prolog el árbol familiar anterior, se puede representar con el siguiente programa, por mencionar solo algunos:

Nota: Dado que prolog no acepta de dos nombres, pues entonces todos los nombres deberían llevar 2. Entonces cambiaremos

-Miguel angel-> Miguel

-Miguel Jr. -> Miguelito

progenitor(francisca, miguel).

progenitor(blas, miguel).

progenitor( fernando, edilia).

progenitor(maura, edilia).

progenitor( miguel, nayeli).

progenitor( miguel, edwar).

progenitor(edilia, nayeli).

progenitor(edwar, miguelito).

Podemos realizar preguntas como las siguientes:

?- progenitor(edilia, nayeli).

?- progenitor(edilia, miguel).

?- progenitor(edwar, miguel).

?- progenitor( X, edilia).

?- progenitor( maura, X).

?- progenitor( X, Y).

1.2. Conjunciones de cláusulas.

Ahora queremos preguntar ¿quién es el abuelo de Miguel Jr?

El programa no incluye la relación 'abuelo', sin embargo podemos hacer la pregunta en dos pasos:

1). Quién es el progenitor de Miguel Jr, asumimos que es algún Y.

2). Quién es el progenitor de este Y, asumimos que es algún X.

Esta pregunta de dos pasos se puede escribir en Prolog:

?- progenitor( Y, miguelito) , progenitor( X, Y).

X = Miguel Ángel

Y = Edwar

la pregunta puede ser entendida como: "encuentra X y Y tal que se satisfagan las dos relaciones simultáneamente".

Si cambiamos el orden de las cláusulas, se produce el mismo resultado:

?- progenitor( X, Y) , progenitor( Y, miguelito).

X = Miguel Ángel

Y = Edwar

INTERESANTE

CREAN EN CINVESTAV LENTES CON INTELIGENCIA ARTIFICIAL PARA INVIDENTES

Con tecnología que conjuga técnicas de geometría computacional, inteligencia artificial, de geoposicionamiento y de ultrasonido, entre otras, científicos del Centro de Investigación y de Estudios Avanzados (Cinvestav) Unidad Guadalajara realizan un dispositivo para ayudar a las personas con debilidad visual o ceguera a desplazarse con mayor facilidad.

Este proyecto, desarrollado en el Departamento de Ingeniería Eléctrica y Ciencias de la Computación, inició de manera formal en 2009, y a menos de cinco años creó un prototipo a punto de transferirse a la empresa jalisciense de tecnología Qualtop, señaló el doctor Eduardo José Bayro Corrochano, líder del proyecto.

El dispositivo de navegación consta de una gafa con cámaras estero-sensores de sonido, tectología de geoposicionamiento GPS y una Tablet, que ayuda a la persona con ceguera a guiarse en su dirección a un punto específico y a evitar chocar contra obstáculos estáticos o en movimiento, además de reconocer billetes de diferentes denominaciones o color de ropa.

El experto, quien también desarrolló el primer robot humanoide de bajo costo en México, llamado Mexone, comentó que fue a partir de avances obtenidos durante sus investigaciones en robótica que consideró emplear los algoritmos de visión estereoscópica para utilizarlos en un dispositivo que guie a personas con discapacidad visual.

La idea surgió a partir de una tesis de doctorado en el Cinvestav Unidad Guadalajara sobre el uso de visión estereoscópica en lentes dirigidos a personas con ceguera. Para ello, los investigadores se acercaron a la Escuela para Niñas Ciegas de Guadalajara A.C., que atiende este tipo de problemática, a fin de conocer las necesidades de los discapacitados visuales.

Fue después del apoyo financiero del Consejo Nacional de Ciencia y Tecnología en 2012 y 2013 cuando pudieron acelerar el desarrollo del lente, configurar del hardware, adaptar los procesadores y probar diferente tipo de sensores empleados en el dispositivo.

“Actualmente tenemos un prototipo liviano, ergonómicamente aceptable ya que casi se ve como una gafa normal y puede trabajar en tiempo real y con baterías que duran aproximadamente cuatro horas de uso continuo. Esperamos tener a más tardar en agosto próximo un prototipo comercial, y a principios de 2015 poderlo comercializar”, expuso Bayro Corrochano, quien también es miembro de la Academia Mexicana de Ciencias.

Según estimaciones del investigador del Cinvestav Unidad Guadalajara, el producto comercial tendría un costo que oscilaría entre mil y mil 500 dólares (13 mil a 19 mil 500 pesos mexicanos), y constaría de la gafa con los sensores y una computadora o tablet donde esté almacenado el software y desde donde una voz dará las indicaciones.

A pesar de que a nivel mundial existan dispositivos similares, a decir de Bayro Corrochano, el desarrollo del Cinvestav Unidad Guadalajara conjuga algoritmos nuevos y tecnología que lo hace único. Por ejemplo, el uso de técnicas de ultrasonido para detectar obstáculos y aquellos translúcidos, como el vidrio, o el empleo de inteligencia artificial (machine learning) con el objetivo de reconocer lugares, letreros y objetos. Estas gafas son útiles también para aquellos de vista débil, ya que ayudan a mejorar la percepción.

El proyecto ha generado dos patentes ante del Instituto Mexicano de Propiedad Industrial, por lo que sus desarrolladores están en busca de inversores interesados en participar en su producción a gran escala.

http://www.invdes.com.mx/tecnologia-mobil/4531-crean-en-cinvestav-lentes-con-inteligencia-artificial-para-%20%20invidentes